How To Make A Conjecture
EXAMPLES, PATTERNS, AND CONJECTURES
Mathematical investigations involve a search for pattern and structure. At the get-go of an exploration, nosotros may collect related examples of functions, numbers, shapes, or other mathematical objects. As our examples grow, we endeavour to fit these individual pieces of information into a larger, coherent whole. Nosotros notation common properties of our examples and wonder if they apply to all possible examples. If further testing and consideration atomic number 82 us to strengthen our belief that our examples reflect a more general truth, then we country a conjecture. The Latin roots of "theorize" interpret to "throw together"—nosotros are throwing together many observations into one thought. Conjectures are unproven claims. Once someone proves a conjecture, it is called a theorem.
You lot can innovate the ideas and activities discussed below equally the need for them arises during educatee investigations. If a educatee uses a particular technique, highlight that approach for the grade. Once a conjecture is posed, ask the class what they demand to do to empathize it and begin to develop an outline that all tin can utilise. Regular opportunities for practice with the different skills (organizing information, writing conjectures, etc.) will pb to greater student sophistication over time.
GENERATING AND ORGANIZING EXAMPLES
Generating Examples
In order to get a improve view of the "large" picture of a trouble, we try to produce examples in a systematic fashion. Nosotros often have to choose examples from an infinite domain. These examples should be representative, in ways that we deem significant, of all of the elements of the domain. For example, a problem involving real numbers might involve positive, negative, whole, rational, and irrational examples. Numbers that are less than one or of bully magnitude might as well be important. In addition to this wide sampling, nosotros also desire to generate examples in a patterned mode so that relationships betwixt variables stand out (see Organizing Data below).
For some problems, examples are easy to produce. At other times, it is not clear if the objects described even exist or, if they do exist, how to construct them. For example, a educatee interested in the parity of the number of factors for each counting number might accept difficulty finding numbers with an odd number of factors. Her search for examples will probably lead her to wonder why about numbers have an even number of factors and perhaps guide her to the atmospheric condition that yield an odd number of factors. This intertwining of discovery and agreement is common throughout mathematical work—proofs often co-evolve with the discoveries themselves.
Information technology is of import to determine when examples are actually different from one another. If we are unable to state what characteristics really matter for a particular trouble (due east.g., order or shape), so we will not be able to figure out when nosotros have enough examples, whether whatever others remain to be establish, or what the sample space that we are searching is. For example, students may find it challenging to generate a diagram that matches the following conditions or to decide whether their examples are even singled-out from each other:
Draw a map showing towns and roads such that:
- Each pair of roads has exactly one town in mutual.
- Each pair of towns has exactly one road in common.
- Every town is on exactly iii roads.
- Every road contains exactly three towns.
As neighbors compare their maps, ask them to consider in what ways the maps differ and in what ways they match. What characteristics count when they consider two maps to exist the aforementioned? As with the rectangle trouble below, we often attend to the topology of a mathematical object more than than to its exact measurements. An object'southward topology is dependent on how its parts are connected to each other.
Being Systematic
We may observe many solutions to a trouble merely withal miss interesting ones if we are non systematic in our search. In order to be systematic, nosotros have to create a path or paths that volition have u.s.a. through all of the possibilities that might ascend. Staying on the path may require an algorithm that guides united states through the choices that nosotros face along the style. The algorithm itself may not be apparent until we accept tried to generate an ordered list and omitted or over-counted some examples. Only, subsequently first experimenting, may we start to understand the internal logic of a trouble.
For practice, students can consider the following question:
A course is investigating subdivisions of a rectangle into north smaller rectangles. They are working on the specific case of dissecting a rectangle into 4 rectangles. What layouts are possible for these subdivisions?
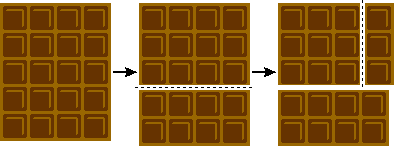
A complete search for even this small case of four rectangles requires careful reasoning. We can consider all possibilities more efficiently by picking a single corner equally our starting point. Recognizing the symmetry of the state of affairs (a rotation or reflection makes the called corner equivalent to the other three) simplifies our work. There are ii ways to put a rectangle in this corner: forth an unabridged side or not (figure one). Again symmetry comes to our aid—it does not matter whether the unabridged side that we comprehend is oriented horizontally or vertically.
Of grade, if nosotros are going to appeal to symmetry, we have to define what we mean past a distinct respond. It is articulate that there will be an infinite number of solutions if the size of the subdivisions is taken into consideration. So, it makes sense to inquire how many categories of these subdivisions there are when we ignore the size of segments and the overall orientation of the figure and just look at the topological relationship between the sub-rectangles (how they edge on i another).
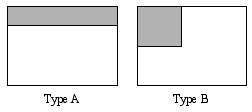
Figure 1. The showtime rectangle is placed in the top left corner
In one case we have the 2 starting arrangements, we take to add iii more rectangles. For the rectangle on the left, we are just left with a smaller version of our original trouble—dissecting a rectangle (the remaining space) into three rectangles. There are just two different ways to perform such a autopsy (test this claim yourself!). Nosotros can rotate these three-rectangle arrangements to generate new candidates for subdivisions using four rectangles (figure two). 1 indistinguishable solution arises (the crossed-out picture is a equivalent to the ane in the upper right corner), and then there are five variations thus far.

Figure ii. Completing a type A rectangle
Nosotros can complete the blazon B rectangle in two boosted unique ways (figure three).

Effigy 3. Completing a type B rectangle
Another valuable technique for generating examples is to build them up inductively from those of a smaller case. We can produce the seven subdivisions found above by bisecting i sub-rectangle in the iii-rectangle subdivisions (figure 4).
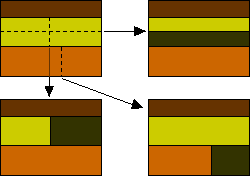
Figure four. Three rectangular subdivisions are turned into iv
This inductive approach works nicely when finding all polyominoes made using n squares from the ready of polyominoes fabricated with n – 1 squares. The n-square polyominoes are institute by adding one boosted square to each available edge of those fabricated with n – 1 squares. However, this inductive arroyo does not work dependably for the rectangle subdivision problem. Subdividing one rectangle of a four-rectangle layout cannot generate the 5-rectangle subdivision pictured below (figure v). This trouble demonstrates that nosotros must thoughtfully choose the methods that we use to generate examples if nosotros want to identify all cases of interest.
Meet Testing Conjectures, below, for a further give-and-take of different types of examples.

Effigy five. A special subdivision
Organizing Data
The examples that nosotros produce in our investigations provide us with data. We try to organize that data in a style that will highlight relationships among our problem's variables. Although there are no guaranteed methods for discovering all patterns, there are some useful basic methods. Numerical data can be organized in tables that facilitate our search for familiar patterns. In a problem with 2 variables, 1 dependent on the other, the information should be listed co-ordinate to constantly increasing values of the dependent variable. For example, a educatee wondered about the number of regions formed by the diagonals of a regular north-gon. She systematically listed the number of sides of the polygons and the number of regions created (figure vi). This substantially one-dimensional arrangement facilitates the discovery of any recursive or explicit functions that relate the two variables.
| north | Regions |
| 3 | 1 |
| 4 | 4 |
| v | eleven |
| half dozen | 24 |
| seven | fifty |
Effigy 6. A table of the number of regions made by the diagonals of a regular northward-gon
Sometimes a problem volition take several independent variables (the values that they can take are not constrained by the other variables). In such cases, we can organize our information past using each dimension of a table to stand for the values of i variable. For instance, in 1899, Georg Pick published a formula that gave the area for a polygon whose vertices lie on the points of a foursquare lattice (figure vii). He discovered that the area could be determined based solely on the number of lattice points inside the interior (I) and on the purlieus (B) of the polygon. His formula was A = 1/2 B + I – 1.

Figure 7. A polygon with two interior and x boundary points has surface area 2 + one/2(10) – 1 = 6
There are several steps one might take toward making such a discovery. 1 might begin with the intuitive notion that the area of a region might exist related to the number of lattice points inside the figure. Then one needs the insight that the area might exist a function of just 2 variables—that it does non depend on the detail shape of the polygon or the number of vertex points. Perhaps this conjecture arises past looking at several examples for the aforementioned B and I. Once this fact is discovered, areas tin exist institute for shapes with unlike combinations of boundary and interior points (effigy viii). A class can use this table to attempt to find Choice'due south formula themselves. Have them draw, or utilize geoboards to make, shapes that see the requirements of a given (B, I) pair and notice the areas of those shapes. (Note: finding the area can be a proficient challenge all by itself—a potentially helpful suggestion is to subdivide the polygon into simpler shapes or draw the rectangle that circumscribes the shape and subtract away excess areas).
| Points in the interior (I) | Boundary points (B) | ||||||
| 3 | 4 | five | half dozen | … | |||
| 0 | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| … | |||||||
Figure 8. A two-dimensional table for organizing information for Pick's theorem
As the table is filled in (figure 9), students may note diverse patterns. They may state what they see recursively (east.one thousand., "Y'all add together one one-half each fourth dimension yous move over a box.") or explicitly ("When B is four, the area is one more than the number of within points."). Both of these forms tin can be helpful in developing a general solution. Encourage your students to write formulas for each row and column and so try to combine these sub-rules into one that works for all (B, I) pairs. It is of import for students to realize, however, that their formulas are conjectures rather than theorems. A proof that the formula ever works is a very challenging task that cannot be based on the data from a finite number of examples (simply you might encourage them to endeavor to prove information technology for easier special cases of polygons such as rectangles, right triangles, etc.).
| Points in the interior (I) | Purlieus points (B) | |||||||
| 3 | 4 | 5 | six | … | B | |||
| 0 | 1/2 | i | 1 one/2 | 2 | ||||
| one | 1 1/ii | 2 | two 1/two | 3 | B / two | |||
| 2 | two 1/2 | 3 | 3 i/ii | 4 | ||||
| 3 | three ane/2 | 4 | 4 1/2 | five | ||||
| … | ||||||||
| I | I + 1/2 | I + 1 | ||||||
Figure ix. A ii-dimensional table for organizing data for Pick's theorem
When a problem has many variables, or a large number of possible values for each variable, it can be difficult studying all combinations systematically. In such cases, we tin choose to agree one (or up to all simply one) variable constant and study the others. In doing so, nosotros are changing the problem to one of a more manageable size. For example, in the Option data above (figure 9), a educatee might kickoff study the column for 4 boundary points (B is held constant while I is allowed to vary). The rule that describes that column, I + one, does not, past itself, give the states a formula for the unabridged table. We must also hold our first variable, B, constant for some new values and then repeat our analysis for fixed values of I while varying B.
The Connect the Dots research setting provides an additional instance of the value of temporarily holding a variable abiding. Students typically hold the dot number constant and generate the diagrams for all jump sizes. Ultimately, we hope to fit all of our findings from these narrower investigations into one larger issue that solves the original problem. For examples of graphical approaches to displaying information to find connections, encounter Graphs in Representations.
LOOKING FOR PATTERNS
We organize the observations that we brand in society to develop conjectures virtually the behaviors of the mathematical objects that nosotros are studying. Once we believe that a blueprint is established, we will land it as a conjecture about an entire class of objects.
Variables That Alter Predictably
As we organize our data, nosotros look for patterns and for ways of describing those patterns formally. Students learn about a variety of familiar patterns (linear, exponential, periodic, etc.) in their algebra classes. Techniques for identifying these patterns and activities that assistance them develop the addiction of using these techniques should be primal to this study. A good resources for teaching the characterization of different patterns is the first chapter of Mathematical Methods (http://www.its-about-time.com/htmls/mm/mm.html) before long to be published by Its Almost Time (http://world wide web.its-about-time.com).
Simplifying a Trouble
Issues can be and then intellectually challenging or computationally enervating that nosotros cannot solve them straight. For example, a student reading Flatland wondered virtually the lengths of the diagonals of a hypercube. What were the longest segments that could fit in such a figure? She began past looking at the lower dimensional versions of the trouble. For a betoken, which is a 0-dimensional "cube", the length of the longest fitting segment is 0. For a unit of measurement segment (the 1-dimensional "cube"), the length of the longest segment is ane. For a unit foursquare, we can fit a diagonal of length ![]() and for a unit cube, the distance from 1 corner to the reverse one is
and for a unit cube, the distance from 1 corner to the reverse one is ![]() (figure 10). Recognizing that 0 and i are both their ain square roots, she extrapolated her blueprint and decided that the diagonal of a unit, 4-dimensional hypercube must exist
(figure 10). Recognizing that 0 and i are both their ain square roots, she extrapolated her blueprint and decided that the diagonal of a unit, 4-dimensional hypercube must exist ![]() or 2. Her pattern did not plant a proof, but the report of simpler related cases guided her to a solution and, ultimately, to a proof for any dimension.
or 2. Her pattern did not plant a proof, but the report of simpler related cases guided her to a solution and, ultimately, to a proof for any dimension.
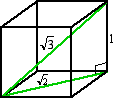
Figure 10. The diagonals of a unit segment, foursquare, and cube
In the hypercube instance in a higher place, the student used smaller cases because she could not, at beginning, visualize the situation that interested her. Using a smaller case is especially important if you find yourself attempting a brute strength solution to a trouble. For example, instead of counting all of the possibilities for a five push simplex lock, 1 of the project hints is to first find a pattern for locks with fewer buttons.
Problems can exist fabricated simpler using a smaller number, simpler shape, or more symmetric setting or shape (e.thousand., a square rather than an arbitrary quadrilateral). They tin can sometimes be made simpler by removing restrictions that seem to make them harder. For instance, the trouble "In how many unlike ways tin an elevator leave the footing floor of a 20 story edifice, make 10 stops moving merely upward, and arrive at the top floor?" is more difficult than the problem that allows the elevator to motion in either management during its stops. For a further give-and-take of methods for creating related bug, see Ways to Change a Problem in Problem Posing. For a form activity that raises questions about how a simpler trouble can be used to solve a more than complex ane, see the section Engineering and Magnitude in the Numbers in Context affiliate from the book Mathematical Modeling available from www.meaningfulmath.org (note: this affiliate is a 1 megabyte downloadable pdf file).
Invariants – Quantities, Objects, and Relationships That Stay the Same
While we often seek to describe how some variable is irresolute, sometimes we want to testify that a characteristic is unaffected by changes in a variable. For example, the ratio of the circumference of a circumvolve to its diameter remains unchanged even as the circle'southward size varies. This fact is obvious one time you study it, only can exist a surprise to children when they kickoff discover it. A belongings or quantity that does not change while other variables are irresolute is called an invariant . The notion of invariance is important throughout mathematics.
Even shapes much less constrained in their grade than circles accept invariant properties. For example, if nosotros construct squares on the sides of a quadrilateral, the segments connecting the centers of the squares on contrary sides volition exist both equal in length and perpendicular (Aubel's theorem, figure 11). Invariants oft prove surprising and stimulate further investigation and explanation. When such consistency appears in the face of asymmetry and variability, we want to detect out what accounts for this dependability.
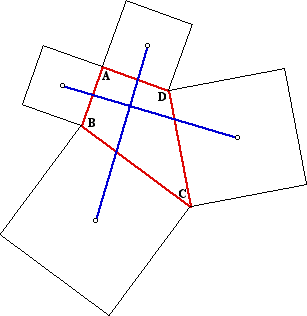
Figure 11. For any quadrilateral, the blue segments are equal and perpendicular
The identification of invariants tin exist a very powerful tool because it lets the states find common properties of situations that look very different. The identification and utilize of invariants becomes more natural with experience. Here are two examples that provide a fuller picture of this concept:
An Algebraic Invariant — Consider the polynomial equation 0 = x 2 + x + a with a constant. We can use the quadratic formula to detect the solutions: ![]() . The sum of these solutions is –1. Therefore, the sum of the solutions to 0 = x 2 + x + a is invariant with respect to a. Similarly, you lot can show that the sum of the solutions of 0 = cx 2 + bx + a is invariant with respect to the constant term a and that the product is invariant with respect to the linear coeeficient b.
. The sum of these solutions is –1. Therefore, the sum of the solutions to 0 = x 2 + x + a is invariant with respect to a. Similarly, you lot can show that the sum of the solutions of 0 = cx 2 + bx + a is invariant with respect to the constant term a and that the product is invariant with respect to the linear coeeficient b.
A Combinatorial Invariant — Suppose nosotros start with a permutation (or reordering) of the numbers 1 through nine:
{6, 8, ane, 9, 3, 7, 5, 4, two}
At that place are many different means to adapt these numbers in ascending society past exchanging pairs. You could offset by exchanging the ix and 2 to give you:
{vi, viii, 1, ii, 3, 7, 5, 4, ix}
Someone else might commutation the 8 and the 2 in the original ordering to get
{6, 2, one, nine, 3, 7, five, iv, 8}
No matter what you do first, go on switching pairs until a final substitution produces
{1, 2, iii, iv, 5, half-dozen, 7, viii, nine}
Try this with some numbered tiles or scraps of paper and keep track of the number of exchanges that y'all make. The number of steps might vary, simply you will always take an odd number of steps. We say that the parity of the original permutation is odd as opposed to existence even if sorting the numbers took an even number of steps, as is the case for {5, 2, 4, ix, 1, three, 6, 7, 8,}. The parity of a permutation is invariant with respect to the exchanges you perform to sort the permutation.
An Activity with Invariants
Consider the following trouble (from Breaking Chocolate Bars at http://www.cut-the-knot.com/proofs/chocolad.html) involving a candy bar that divides into m by northward small squares (figure 12). Starting with a whole bar, a move consists of choosing a slice of the bar and breaking it forth one of the horizontal or vertical lines separating the squares. The two new pieces are so returned to the pile to be available for the next move.The claiming is to find the fewest number of moves needed to break the bar into all private (1 by 1) squares.
Effigy 12. A 4 past v chocolate bar and ii possible first moves
Innovate this situation to your course and have each pair of students option bars of a detail size and proceed track of the number of moves needed each time. They can carry out their investigations cutting pieces of graph paper, separating sections of an array of interlocked cubes, drawing segments on a grid, or breaking an actual chocolate bar. Ask them to consider whether certain strategies for choosing which slice to break seemed more efficient than others.
After several tries, it should become credible that, for a given size bar, the number of moves required is e'er the same. Why is the outcome invariant with respect to the sequence of breaks? What does impact the number of moves needed? At this juncture, you can guide your grade in 1 of two directions. They can be asked what variables touch the number of moves and be given time to find a rule that predicts that total—they may retrieve about organizing the possibilities for different values of thou and n in an array or try looking at specific small cases. Alternatively, and this is the faster route, yous can ask them to keep track of the number of pieces after each cut. You may even want to do both of these analyses in order.
The key observation is that the number of pieces of processed is always one more the number of moves considering each move adds ane more piece. That is, the number of pieces is invariant with respect to the choice of breaks fabricated. This invariance tells u.s. that we will always cease upwardly with mn pieces after mn – 1 moves. This activity provides a nice example of how we can use invariants as a tool for constructing proofs.
For additional teaching material related to invariants, see Affiliate ane lessons 7, 8, and x in the book version and lessons 14, 15, and 16 in the CD-ROM version of the Connected Geometry curriculum (http://world wide web.everydaylearning.com/geometry). Yous can also download Tackling Twisted Hoops, an commodity on invariants and knot theory from the quondam Quantum magazine.
A Different Kind of Observation
Although the almost common kind of discovery for secondary students engaged in mathematics inquiry to make is ane about numerical patterns, there are other kinds of possible conjectures. One type of observation could be that a pattern or arrangement that they are studying has been encountered in some other context. Such an observation can lead to a conjecture that there is a common explanation for the two apparently dissimilar questions and to a way of showing that the two are related in some fashion.
I such enquiry began when another student who was inspired by Flatland looked at the number of vertices in an northward-dimensional cube a given distance away from a chosen vertex. The distance was measured by travelling but along the edges of the figure. For example, if a corner of a square is chosen, then in that location is one point 0 steps away (the point itself), two vertices that can be reached by travelling along a unmarried edge, and i vertex a altitude of ii edges away (figure xiii).
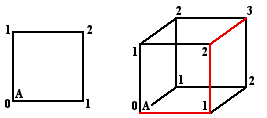
Effigy xiii. The altitude along the edges from vertex A in a square and a cube
When the student organized his data in a table (figure xiv), he saw a familiar sight. He so conjectured and set out to explain the connection between n-dimensional cubes and Pascal's triangle.
| d | Point | Segment | Foursquare | Cube | Hypercube |
| 0 | 1 | 1 | 1 | i | i |
| 1 | 0 | 1 | two | 3 | 4 |
| 2 | 0 | 0 | i | three | half-dozen |
| iii | 0 | 0 | 0 | 1 | four |
| 4 | 0 | 0 | 0 | 0 | ane |
Figure fourteen. The number of vertices distance d abroad from a vertex in each shape
For further discussion and settings that encourage the making of such connections, meet Practice Activities in the Proof section.
Understanding CONJECTURES
We seek to understand a conjecture at three levels: we desire to determine its significant, we want to identify reasons for why we might believe the claim to be true, and nosotros want to understand how it fits within some larger set of ideas. The initial steps we take when exploring a conjecture are like to those used to empathise a definition:
- Read the statement more than than once. Important subtleties are often missed on the first read.
- Identify each of the atmospheric condition of the theorize. A conjecture's conditions are those criteria that must be satisfied before we take the conclusions of the conjecture. They are the if part of the statement. Each substantive and adjective may constitute a specific status.
- Generate examples and non-examples. Find objects that meet the conditions and check to see that they also satisfy the decision of the conjecture. Remove each status in plough and construct non-examples that satisfy the other conditions but not the decision. Non-examples help united states empathise the importance of each status to the conjecture. Conditions constrain the objects under consideration to a set up that all share particular backdrop.
- Look for counterexamples. A counterexample satisfies all conditions of a statement but not the conclusion. Exercise the conditions leave "wriggle room" for an object that fails to satisfy the decision of the conjecture? If a counterexample does exist, then the conjecture is imitation.
- Compare. How is this conjecture related to other statements virtually the same or similar mathematical objects?
The same steps help when nosotros are familiarizing ourselves with a new theorem. In the case of a theorem, we want to read and understand the proof likewise. In the case of a conjecture, we are looking for evidence that would support a proof or provide a path to a disproof.
Removing weather condition
The Angle-Angle-Side (AAS) Congruence Theorem: If, in 2 triangles, two angles and a non-included side of one triangle are congruent respectively to two angles and the corresponding non-included side of the other, then the triangles are congruent.
The AAS theorem has many weather. It involves triangles, 2 angles, one side, the side'southward position relative to the angles, congruency, and correspondence. In order to meet why each one is necessary, we need to remove each condition and and then create a pair of triangles that satisfy the remaining conditions but are non congruent. For example, if we remove the status that the figures are triangles, we can construct different quadrilaterals that share ii congruent angles and an equal non-included side. The table below (effigy fifteen) shows non-examples for three dissimilar conditions.
| Status Removed | Non-examples |
| Figures are triangles. | |
| Two angles must be congruent. | |
| Congruent side must be the corresponding not-included one (these triangles are similar but not congruent). | |
Figure 15. Non-examples for the AAS theorem
As a class activity, present theorems and conjectures and ask students to first list all conditions of the statement then produce non-examples for each. Two claims that they can practice with are (1) If a and b are positive integers, d is the greatest common gene of a and b, and c is not divisible by d, then in that location are no integral solutions to ax + by = c and (ii) If an odd integer is raised to an odd integral power, then the result is an odd integer. Do not tell your form ahead of time that the first merits is a theorem while the 2nd is a false conjecture. Students will get boosted practise understanding the conjectures that their peers generate throughout the year.
EVALUATING CONJECTURES
What are the possible characteristics of a conjecture and what makes ane conjecture more interesting than others? Students should explicitly answer each of the following questions when they seek to evaluate a conjecture:
- Does the conjecture appear to exist true or false?
Nosotros rarely have a definitive answer to this question right abroad, but our understandings of related results may guide our intuitions. A report of examples and a search for counterexamples will further influence our belief in the truth of a theorize. Students tend to be too decumbent to believe that a few examples establish irrefutable show of a pattern.
- Is information technology obvious or subtle?
If a conjecture immediately follows from a known upshot, and then it may be less interesting than an unexpected conjecture. For example, a claim virtually squares may not be exciting if a pupil has already proven the same merits for a superset such as parallelograms.
- Is it easy or difficult to understand?
A conjecture may exist hard to sympathize because of the way information technology is written or because the mathematics involved is inherently complicated. Students should re-write their conjectures if their mathematical language is unnecessarily confusing.
- Is the conjecture general?
A conjecture that, if true, applies to a broad range of objects or situations will exist more significant than a limited claim. Does it advise a connexion between two different topics?
- Is it specific enough?
A 2nd-grader was investigating which northward past m boards could exist tiled past the T-tetromino (four squares arranged edge-to-edge to wait like a capital T, figure 16).

Figure 16. A iv past 8 board tiled with T-tetrominoes
Her ultimate conjecture, "If the sides of a lath are even by fifty-fifty information technology may work, if not then not," left her dissatisfied. She correctly believed that any odd dimension fabricated the tiling impossible, but she knew that evenness was not a precise enough status to distinguish betwixt all of the boards that did and did non tile. She knew that if she could refine her weather condition her conjecture would be stronger. (Run into Necessary and Sufficient Conditions below.)
- Do you like the conjecture? Practice you discover it appealing?
People are attracted to different mathematics questions. Information technology is important for students to begin to develop their own aesthetic for mathematical ideas and to understand that aesthetics play a role in the discipline. Conjectures that are unexpected or counter-intuitive, that reveal a complex pattern, or that would be useful in supporting other of import conjectures are more likely to exist appreciated by a wide audience.
TESTING CONJECTURES
The showtime question that nosotros confront in evaluating a conjecture is gauging whether information technology is true or not. While confirming examples may help to provide insight into why a conjecture is truthful, we must also actively search for counterexamples. When students believe a theorize, they are non always rigorous in their search for examples that break the pattern that they have identified. We must help them develop the habit of existence more than skeptical. 1 mode we tin can develop this skepticism is by giving students problems that take "false" patterns—ones that seem familiar merely do non continue as expected (see Conjectures Are Not Theorems below).
How can students search for counterexamples? They should exam cases between those that they have found to work. They should look at extreme cases at the far ends of the domains of their issues (e.chiliad., obtuse triangles that are most apartment or numbers near zero). They should consider degenerate cases that practice not take all of the complexity of a typical example. Degenerate cases oftentimes result from making some parameter zip. For case, a signal when the conjecture applies to circles (the radius has been set to zero) or a linear equation when the topic is quadratics (the coefficient of the squared term is zero). A quadrilateral is a degenerate pentagon in which two of the points are in the aforementioned location. Of course, some degenerate cases are not actually relevant to a problem (e.g., ellipses tin exist defined in terms of a focus and directrix, just circles cannot).
In addition to farthermost and degenerate examples, we should besides generate and test special cases. Special cases possess an boosted property, such every bit symmetry, that most other cases lack. A foursquare is a special rectangle and correct or isosceles triangles are distinct cases to investigate. In other contexts, special cases might be numbers with no duplicate prime number factors, matrices with a determinant of 0 or ane, or functions that are monotonic.
Before a course investigates new conjectures, I nowadays them with a old student's summary: "A theorize has 3 possible fates: life, death, and limbo. Life is gained through proof, expiry by counterexample, and limbo is just limbo. Death can lead to rebirth through refinement." This pithy statement emphasizes that a single counterexample is sufficient to impale a conjecture and that proof—not a slew of examples or the absenteeism of a counterexample—is the simply way we tin can be certain of a claim.
Students should non see the discovery of a counterexample as a failure. It is both a sign of their thoughtfulness and the possible start of a new and better theory. A counterexample may disprove a conjecture, just it does not mean that the merits is always imitation. A theorize may exist well-nigh e'er true. Conjectures are reborn when we identify what extra condition removes the possibility of counterexamples or what part of our conclusion we need to brand less specific. For example, a geometry educatee's theorize that "the intersections of the angle bisectors of a parallelogram form a rectangle in the interior of the parallelogram" was salvaged by classmates who pointed out that the give-and-take "interior" made counterexamples possible. Another students' conjecture, "The perpendicular bisectors of the sides of a kite do non intersect in a signal," works for most kites but needed the additional condition that the non-terminate angles non be right angles. Students should group their counterexamples and confirming examples and look for a holding that distinguishes the two sets.
For a form activity that involves looking for counterexamples, see the section Understanding Definitions: Closed and Dense in the Numbers in Context chapter from the volume Mathematical Modeling.
WRITING CONJECTURES
For students, there is oft a wide gulf between the ideas with which they can grapple and their ability to write a clear argument of their thinking. They need to acquire the mathematical vocabulary and formal structures that brand writing a logical claim easier. They make that progress when we provide them with aplenty opportunity to recognize, write, and refine conjectures. The following describes a sequence that provides do creating and reworking conjectures.
Form Activity
Dynamic geometry programs, such as Geometer's Sketchpad ® or Cabri Geometry II ™, that permit students to construct accurate diagrams of geometrical objects take become pop tools for classroom investigations. If students are given some flexibility in the settings that they explore, they will happily struggle with complicated conjectures that tin can exist a valuable focus of grade discussion. Consider the post-obit sampling of claims, ranging from m to muddled, that were generated past students. The conjectures were responses to an consignment to choose a form of quadrilaterals and to identify whatsoever backdrop of the angle bisectors or perpendicular bisectors of the sides of those figures.
- The intersections of the perpendicular bisectors of a parallelogram create a new parallelogram with the same angle measures as the original.
- The angle bisectors of a rectangle brand a square.
- All of the perpendicular bisectors of an isosceles trapezoid intersect at the same point. That point of intersection is the center of a circle which contains all of the vertices of the isosceles trapezoid.
- In a trapezoid, the angles formed at the intersection point of the longest base line and the non-base angle bisector are congruent only if both angles are outside or both are outside.
- In an isosceles trapezoid, the base angle bisectors create an angle equal to the opposite base angle.
- In a trapezoid, two coinciding triangles are made by the bisectors of consecutive non-base angles and where one intersects the base line.
- In a kite, where all the angle bisectors run across is the heart.
- In a trapezoid, the angles formed at the intersection point of the longest base line and the non-base of operations angle bisector are congruent only if both angles are inside or both are exterior.
- In a trapezoid, the two base angle bisectors brand an isosceles triangle at the bespeak of intersection.
- If the angle bisectors of a quadrilateral form a rectangle, and then that figure is a parallelogram.
- An isosceles trapezoid'due south angle bisectors create four congruent correct triangles.
Later on two or iii days of laboratory time, each group submits their lab report with examples and conjectures. To make sure that they clearly define what they are describing, they are not allowed to apply labels from the figures; they had to apply accepted vocabulary. The next twenty-four hours each student is given a folio of conjectures, such equally the above list, drawn from the reports. They read the conjectures and attempt to understand them, to generate test cases, and to evaluate them according to the standards noted in a higher place (run into Evaluating Conjectures).
The class and then discusses each conjecture. Anonymously, students heed to what their peers think nearly the clarity of their writing and the success of their conjecture. Students provide effective advice on how to clarify each statement. An reward of peer review such equally this to teacher comments is that students are ordinarily quite adept at finding alternative interpretations of confusing statements that reveal the imprecision in a claim. Often, a form will have several interpretations amongst which it cannot make up one's mind. This predicament helps the author effigy out how to modify their conjecture to say what they intended. A cycle of peer evaluation and rewriting leads to meliorate conjectures and improve self-edited conjectures in the hereafter.
Peer review of first drafts is preferable to teacher evaluation because teachers are as well good at figuring out what a pupil "actually meant" mathematically. Peers proceed the initial focus where it belongs, on the act of articulate communication. Grade discussions almost the subtlety, difficulty, and appeal of a conjecture pb to fewer lilliputian conjectures as the year progresses. These benefits of the peer review procedure also aid the class develop a sense of itself equally a mathematical customs.
Sometimes a class volition provide counterexamples to signal out that a conjecture is false or will fail to make whatsoever sense of a conjecture (see which of the examples above make sense to you). If a theorize is adequate, instructor feedback can so address bug such as choice of vocabulary and the evolution of symbolic representations that simplify a statement. Refined conjectures should exist named in honor of their creators (due east.g., "Rahim and Janie's Pentagon Theorize") and posted so that their standing as interesting only unproven claims is highlighted. Students are often particularly motivated to prove their own claims and turn them into theorems.
Conditional Statements
High school texts typically suggest that conjectures and theorems exist written in "if A, and so B" form. All the same, there are many other common forms that for particular conditional statements may exist simpler to country and understand. One difficulty with some of these forms is that they may also obscure what the premise and conclusions of a conditional statement are. Students naturally use a range of forms and can do good from considering culling means of stating their ideas. No unmarried structure is best in all cases.
In their mathematical reading, students will encounter a variety of conditional statements that are nearly identical to standard if and then form. These include: all A are B; A, and so B; if A, B. Let A. And then B; and B, if A. Other conditional statements seem more descriptive than inferential. For example, "the medians of a triangle are concurrent" is preferable but could be turned into "if a figure is a triangle, and so its medians are concurrent." This latter form highlights that the but premise in the statement is having a triangle. Notwithstanding, as illustrated in the educatee quadrilateral conjectures above, information technology is not the most comfy mode to land a wide range of conjectures. Y'all should talk over the different forms for a provisional statement and occasionally recapitulate student conjectures in alternative forms so that students go familiar with them.
Necessary and Sufficient Conditions
A necessary condition is one that must exist met in order for a given conclusion to exist true. However, satisfying the condition does not guarantee that the conclusion is true. When a sufficient condition has been met, then the conclusion for which information technology was a condition will be true regardless of any other properties.
Students are not always attuned to the difference betwixt necessary and sufficient weather. Withal, their conjectures occasionally provide the opportunity to make the distinction. In the tetromino example above, evenness of dimensions is a necessary, but not sufficient, condition for beingness able to tile the rectangle. Knowing that a tiling works for a given board is a sufficient status for knowing that the sides are even (that is, if A is necessary for B, then B is sufficient for A). Come across Sarah'due south Conjectures in the Pedagogy Notes for the Connect the Dots project for some other pupil case.
For a quadrilateral, having diagonals that perpendicularly bisect each other is both a necessary and sufficient status for existence a rhombus. In such cases, nosotros can write "a figure is a rhombus if and only if its diagonals perpendicularly bisect each other." An "if and only if" claim (abbreviated iff) is a compact form for stating a theorize and its converse together.
For further discussion and classroom activities, download Necessary Condition and Sufficient Condition (from Becker (1997) and distributed with permission from the National Quango of Teachers of Mathematics). Meet Logical Relationships Between Provisional Statements in the Mathematics Tools section for a related give-and-take.
CONJECTURES ARE NOT THEOREMS
We are all prone to believe that a pattern that we discover is likely to go on. Our willingness to state a conjecture reflects that conventionalities. Faith, however, is not the same equally truth, and we need to help our students become appropriately skeptical (also as hopeful) nigh their conjectures. When they practice discover that a conjecture is faux, they should still be pleased that they take uncovered a mathematical truth. I remind my classes repeatedly that "an example is not a proof," but but repeating a mantra will non change habits. Students need to experience, early on and frequently, the demise of conjectures nearly which they had no doubt. Such experiences will ascend in the course of their researches, merely we can as well plan them as class activities.
A archetype activity for illustrating the value of skepticism involves ten 2 + 10 + 41. Begin past having students create a table with the starting time dozen or more than values of the polynomial when x = 0, ane, ii, 3, etc. Seek observations and conjectures about the values that arise. All of the values volition be both odd and prime. A student may also note the arithmetic sequence of the differences between the terms. Ask the students whether they believe that this polynomial will always produce odd, prime output. Ask what they would need to see to be convinced one way or some other. If information technology is suggested that further examples be checked, then accept them go along plugging in values for x. be patient. Try to vesture them downwards! Every bit students extend the table, they will meet that the patterns keep. Are they convinced now? How many terms are needed to sway them? How can they actively adopt a skeptical approach? Tin can they actively expect for values of x that might not yield a prime or odd number? Requite them the time to do and then. The first forty terms volition be prime, just the polynomial yields a blended number (41.43) when ten = 41. What if no odd counterexample appears? Might it prove upwardly after millions of confirming examples? Can they prove that the polynomial is always odd for whole number values of x?
An amazing instance that is worth sharing with students is that of ane+1141due north 2 (Sowder and Harel 1998). Are there values for northward that make this expression a perfect foursquare? Every bit it turns out, all n from 1 to 30,693,385,322,765,657,197,397,207 neglect to produce a perfect square. However, if one tries 1+1141.30,693,385,322,765,657,197,397,2082, a perfect square arises. So, not but is an example not a proof, but more than 30 septillion sequent examples should not constitute a convincing argument.
Even an infinite number of examples does not eliminate the possibility of a counterexample. For example, students tin can come with an unlimited number of examples of a rational number divided by a rational number yielding a rational, but the rationals are non closed under division because of 0. Run across the section Understanding Definitions: Closed and Dense and its associated handouts in the Numbers in Context chapter from the volume Mathematical Modeling for boosted word and activities that reinforce the demand for conscientious searches for counterexamples and for proof.
CONCLUSION
Conjecturing can be made a regular strand inside any grade. Any mathematics topic can exist the source of patterns and the chance to generate conjectures. Once students become comfy with the process of developing conjectures, they will start to initiate explorations based on their observations and enquiry will go a daily possibility. In addition to teaching students well-nigh how mathematical knowledge is developed, an emphasis on conjecturing often proves interesting for students. This heightened interest contributes to longer-term recall and mastery of the technical skills that are practiced during the investigations. The relative openness of conjecturing activities also puts students in situations where their confusions or conflicting understandings near an thought are more likely to be exposed and so resolved.
BIBLIOGRAPHY
Abrams, Joshua (2001). Mathematical modeling. Online at www.meaningfulmath.org/modeling.
Becker, Jerry & Shimada, Shigeru (1997). The open-ended arroyo: a new proposal for teaching mathematics. Reston, VA: National Council of Teachers of Mathematics.
Breaking Chocolate Confined is bachelor online at http://world wide web.cutting-the-knot.com/proofs/chocolad.html.
Education Evolution Center (2000). Connected geometry. Chicago, Ill: Everyday Learning Corporation.
Education Evolution Center (2001). Mathematical methods: topics in discrete and precaclulus mathematics. Armonk, NY: It's Near Time.
Matveyev, S (2000, Nov/December). Tackling twisted hoops. Quantum, 8–12.
Sowder, Larry and Guershon Harel (1998, November). Types of students' justifications. Mathematics Teacher, 670–675.
Part of the Conjectures Are Not Theorems discussion is adapted from Mathematical Modeling: Didactics the Open-ended Application of Mathematics © Joshua Abrams 2000 and used with permission.
![]()
Printable Version (PDF)
![]()
How To Make A Conjecture,
Source: https://www2.edc.org/makingmath/handbook/Teacher/Conjectures/Conjectures.asp
Posted by: mattosminquirwas.blogspot.com


0 Response to "How To Make A Conjecture"
Post a Comment